Previous

Simulate a Complete State Estimation Problem

Now, we put all things together we learned so far to build a complete simulation of a target tracking problem using the Nonlinear Estimation Toolbox.

The following CompleteEstimationExample() function simulates a random trajectory of target inclusive noisy measurements based on the previously developed system and measurement models. The target will be tracking using different estimators. Relevant data like the true system state, point estimates, or runtimes are collected and subsequently plotted.

You can set for each filter a color/plotting description, e.g., line style, markers, etc., using the setColor() method. It accepts any data like chars or cell arrays. This allows for easy plotting of estimation results. Of course, this functionality can be abused to associate any other data to a filter instance.

CompleteEstimationExample.m

Simulate a complete nonlinear state estimation problem.
function CompleteEstimationExample()
    % Instantiate system model
    sysModel = TargetSysModel();
    
    % Instantiate measurement Model
    measModel = PolarMeasModel();
    
    % Setup the filters
    filters = FilterSet();
    
    filter = EKF();
    filter.setColor({ 'Color', [0 0.5 0] });
    filters.add(filter);
    
    filter = UKF();
    filter.setColor({ 'Color', 'r' });
    filters.add(filter);
    
    filter = UKF('Iterative UKF');
    filter.setMaxNumIterations(5);
    filter.setColor({ 'Color', 'b' });
    filters.add(filter);
    
    filter = SIRPF();
    filter.setNumParticles(10^5);
    filter.setColor({ 'Color', 'm' });
    filters.add(filter);
    
    numFilters = filters.getNumFilters();
    
    % Initial state estimate
    initialState = Gaussian([1 1 0 0 0]', [10, 10, 1e-1, 1, 1e-1]);
    
    filters.setStates(initialState);
    
    % Simulate system state trajectory and noisy measurements
    numTimeSteps = 100;
    
    sysStates          = nan(5, numTimeSteps);
    measurements       = nan(2, numTimeSteps);
    updatedStateMeans  = nan(5, numFilters, numTimeSteps);
    updatedStateCovs   = nan(5, 5, numFilters, numTimeSteps);
    predStateMeans     = nan(5, numFilters, numTimeSteps);
    predStateCovs      = nan(5, 5, numFilters, numTimeSteps);
    runtimesUpdate     = nan(numFilters, numTimeSteps);
    runtimesPrediction = nan(numFilters, numTimeSteps);
    
    sysState = initialState.drawRndSamples(1);
    
    for k = 1:numTimeSteps
        % Simulate measurement for time step k
        measurement = measModel.simulate(sysState);
        
        % Save data
        sysStates(:, k)    = sysState;
        measurements(:, k) = measurement;
        
        % Perform measurement update
        runtimesUpdate(:, k) = filters.update(measModel, measurement);
        
        [updatedStateMeans(:, :, k), ...
         updatedStateCovs(:, :, :, k)] = filters.getStatesMeanAndCov();
        
        % Simulate next system state
        sysState = sysModel.simulate(sysState);
        
        % Perform state prediction
        runtimesPrediction(:, k) = filters.predict(sysModel);
        
        [predStateMeans(:, :, k), ...
         predStateCovs(:, :, :, k)] = filters.getStatesMeanAndCov();
    end
    
    close all;
    
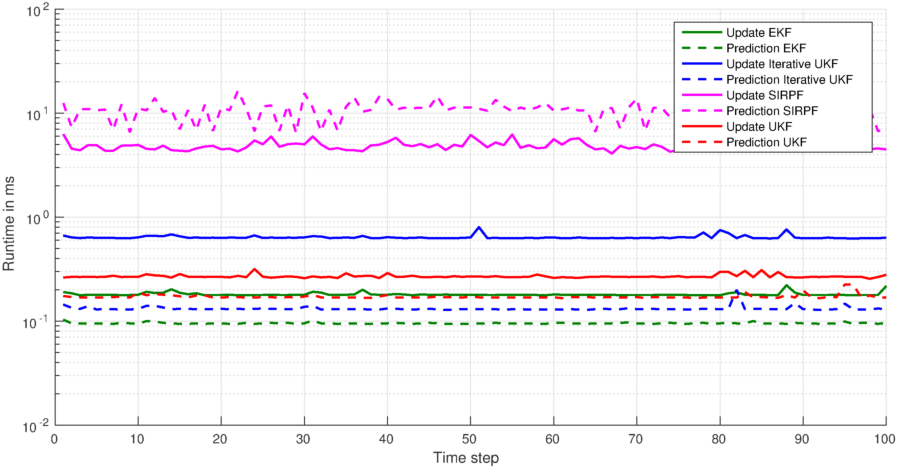
    % Plot state prediction and measurement update runtimes
    figure();
    hold on;
    grid  on;
    xlabel('Time step');
    ylabel('Runtime in ms');
    
    for i = 1:numFilters
        filter = filters.get(i);
        color  = filter.getColor();
        name   = filter.getName();
        
        r = runtimesUpdate(i, :) * 1000;
        plot(1:numTimeSteps, r, '-', 'LineWidth', 1.5, color{:}, ...
             'DisplayName', sprintf('Update %s', name));
        
        r = runtimesPrediction(i, :) * 1000;
        plot(1:numTimeSteps, r, '--', 'LineWidth', 1.5, color{:}, ...
             'DisplayName', sprintf('Prediction %s', name));
    end
    
    set(gca, 'yscale', 'log');
    
    legend show;
    
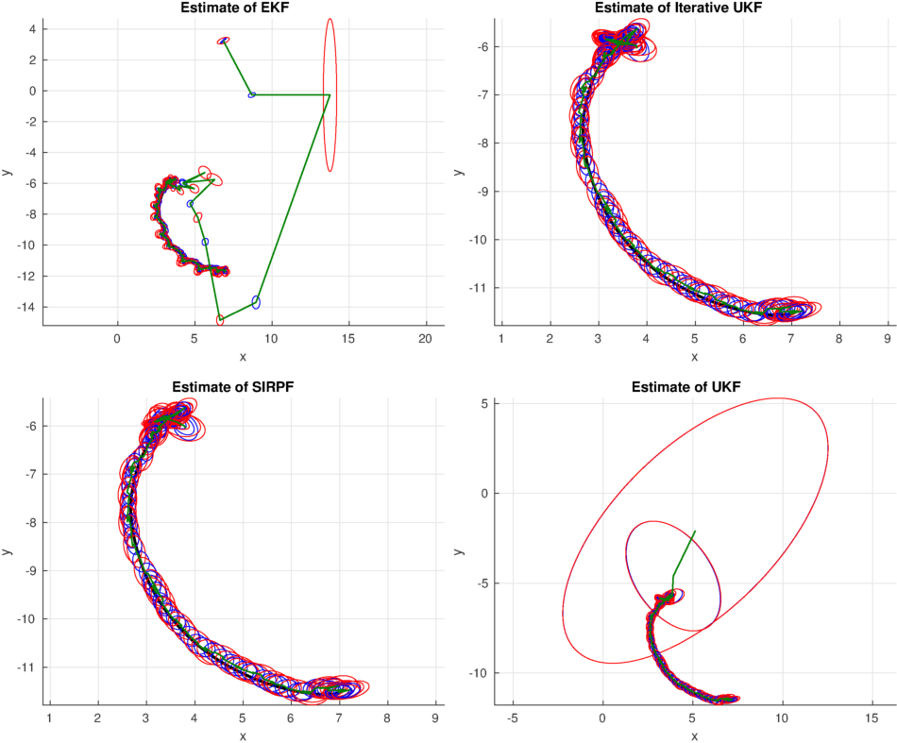
    % Plot state estimates
    figure();
    
    for i = 1:numFilters
        subplot(2, 2, i);
        
        hold on;
        axis equal;
        grid on;
        xlabel('x');
        ylabel('y');
        
        filter = filters.get(i);
        name   = filter.getName();
        
        title(['Estimate of ' name]);
        
        % Plot true system state
        plot(sysStates(1, :), sysStates(2, :), 'k-', 'LineWidth', 2);
        
        % Show confidence interval of 99%
        confidence = 0.99;
        
        objectTrace = nan(2, 2 * numTimeSteps);
        j = 1;
        
        for k = 1:numTimeSteps
            % Plot updated estimate
            updatedPosMean = updatedStateMeans(1:2, i, k);
            updatedPosCov  = updatedStateCovs(1:2, 1:2, i, k);
            
            plotCovariance(updatedPosMean, updatedPosCov, confidence, 'b-');
            
            objectTrace(:, j) = updatedPosMean;
            j = j + 1;
            
            % Plot predicted estimate
            predPosMean = predStateMeans(1:2, i, k);
            predPosCov  = predStateCovs(1:2, 1:2, i, k);
            
            plotCovariance(predPosMean, predPosCov, confidence, 'r-');
            
            objectTrace(:, j) = predPosMean;
            j = j + 1;
        end
        
        % Plot object trace
        plot(objectTrace(1, :), objectTrace(2, :), 'Color', [0 0.5 0], 'LineWidth', 1);
    end
end

function handle = plotCovariance(mean, covariance, confidence, varargin)
    % covariance = V * D * V'
    [V, D] = eig(covariance);
    
    sigma = sqrt(diag(D));
    
    scaling = sqrt(chi2inv(confidence, 2));
    
    if covariance(1, 1) > covariance(2, 2)
        phi = atan2(V(2, 2), V(1, 2));
        
        extent = scaling * [sigma(2) sigma(1)];
    else
        phi = atan2(V(2, 1), V(1, 1));
        
        extent = scaling * [sigma(1) sigma(2)];
    end
    
    handle = plotEllipse(mean, extent, phi, varargin{:});
end

function handle = plotEllipse(center, extent, angle, varargin)
    a = 0:0.01:2*pi;
    
    s = [extent(1) * cos(a)
         extent(2) * sin(a)];
    
    ca = cos(angle);
    sa = sin(angle);
    
    s = [ca -sa
         sa  ca] * s;
    
    handle = plot([s(1, :) s(1, 1)] + center(1), [s(2, :) s(2, 1)] + center(2), varargin{:});
end

Executing the file with

>> CompleteEstimationExample()

and you should get figures like this:

Simulated State Estimation Problem - Results

Results of simulated nonlinear state estimation problem

Simulated State Estimation Problem - Runtimes

Runtimes of simulated nonlinear state estimation problem

At this point, you are familiar with the basic principles of the Nonlinear Estimation Toolbox! Now, you should have a look at the complete list of Estimators available in the toolbox or get an overview of the Probability Distributions, System Models, and Measurement Models not treated here.

Previous